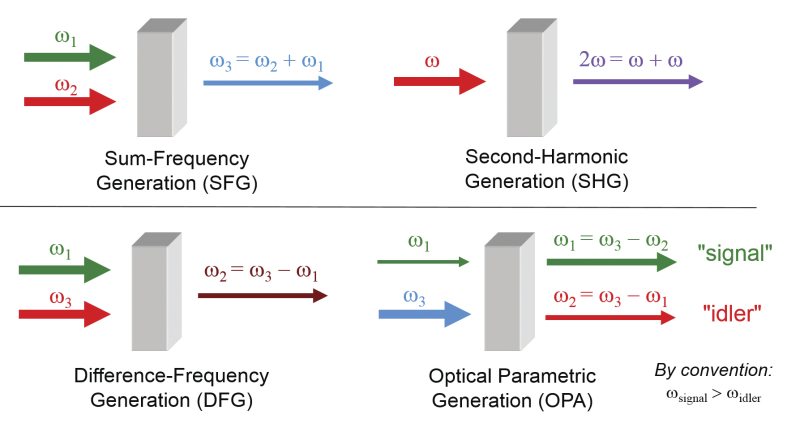
For the case where the polarization is quadratically dependent on the field, these phenomena are known as second-order NLO effects. It is important to note that the two incident optical fields can be from the same laser source and thus possess the same frequency. However, in general, the two fields (sometimes referred to as waves) have different frequencies and, when they interact within the nonlinear medium, they produce a field with a new frequency. This process, known as three-wave mixing (depicted in Figure 3), can take on a variety of forms depending on the input frequencies and the desired output frequency. The upper row of Figure 3 shows the process of sum-frequency generation (SFG) where the input frequencies are added to produce higher frequency (shorter wavelength) light. Second harmonic generation (SHG) is a specific type of SFG that is commonly used since it allows for frequency-doubling of a single laser beam. By contrast, the lower row of Figure 3 shows difference frequency generation (DFG) where smaller frequency (longer wavelength) light is produced. Optical parametric amplification (OPA), a type of DFG, uses a pump beam to produce two waves of lower frequency that can span a wide spectral range. If the nonlinear medium that produces OPA is placed within a cavity, an optical parametric oscillator (OPO) can be formed, which effectively becomes an optically-pumped tunable source.
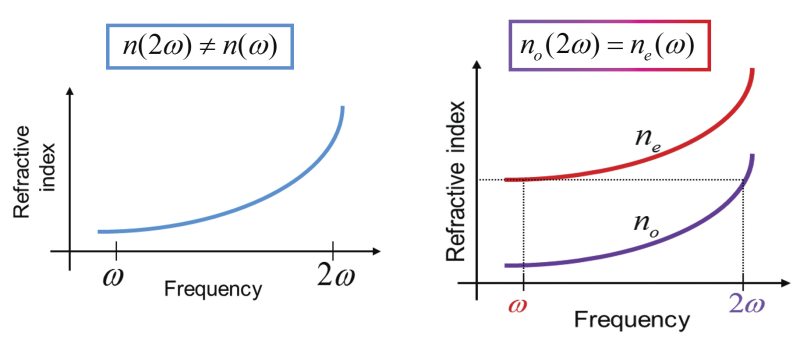
Once the conservation of energy condition is met (as shown by the frequency equations in Figure 3), a "phase-matching" condition must also be met to ensure efficient three-wave mixing. Phase-matching requires that the indices of refraction at the frequencies of the various waves be equal. This allows the three waves to be temporally and spatially overlapped over a long interaction length. An example of phase-matching is shown in Figure 4 for SHG. Due to dispersion, i.e., change in the refractive index with frequency, and the differences in frequencies of the waves, phase-matching cannot be achieved in a material with a single refractive index (see Figure 4, left). However, this can be accomplished by using a birefringent material, that is, a material that has different refractive indices for different input polarizations (see Figure 4, right). The polarizations for the waves must be orthogonal to one another and are referred to as the “ordinary” or o-wave and the “extraordinary” or e-wave, depending on the properties of the birefringent material. Birefringence naturally occur in certain crystalline materials and so NLO materials for three-wave mixing are typically crystals. The optimal phase-matching condition in an NLO crystal can be determined for a specific set of frequencies and polarizations. Wavelength (or frequency) tuning is then accomplished by either changing the orientation of the crystal through rotation or sometimes by adjusting its temperature in order to vary the index of refraction.
 Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details
Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details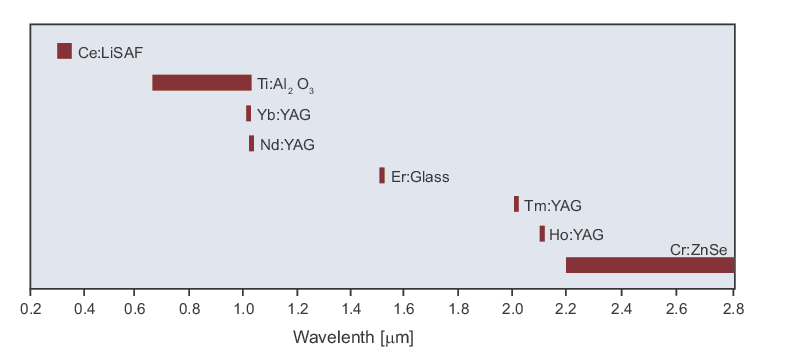

 Ultra-High Velocity
Ultra-High Velocity