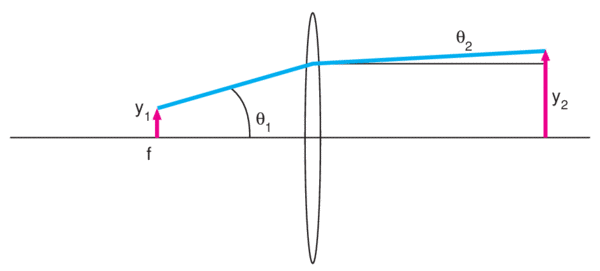
The expansion ratio
y3/y1 = θ2f2/θ2|−f1| = f2/| −f1|
or the ratio of the focal lengths of the lenses. The expanded beam diameter
2y3 = 2θ2f2 = 2y1f2/|−f1|
The divergence angle of the resulting expanded beam
θ3 = y2/f2 = θ1|−f1|/f2
is reduced from the original divergence by a factor that is equal to the ratio of the focal lengths |-f1|/f2. So, to expand a laser beam by a factor of five we would select two lenses whose focal lengths differ by a factor of five, and the divergence angle of the expanded beam would be 1/5th the original divergence angle.
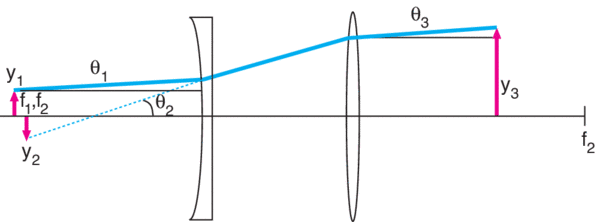
As an example, consider a Newport R-31005 HeNe Laser with beam diameter 0.63 mm and a divergence of 1.3 mrad. Note that these are beam diameter and full divergence, so in the notation of our figure, y1 = 0.315 mm and θ1 = 0.65 mrad. To expand this beam ten times while reducing the divergence by a factor of ten, we could select a plano-concave lens KPC043 with f1 = -25 mm and a plano-convex lens KPX109 with f2 = 250 mm. Since real lenses differ in some degree from thin lenses, the spacing between the pair of lenses is actually the sum of the back focal lengths BFL1 + BFL2 = -26.64 mm + 247.61 mm = 220.97 mm. The expanded beam diameter
2y3 = 2y1f2/|-f1| = 2(0.315 mm)(250 mm)/|-25 mm|= 6.3 mm
The divergence angle
θ3 = θ1|-f1|/f2 = (0.65 mrad)|-25 mm|/250 mm = 0.065 mrad
For minimal aberrations, it is best to use a plano-concave lens for the negative lens and a plano-convex lens for the positive lens with the plano surfaces facing each other. To further reduce aberrations, only the central portion of the lens should be illuminated, so choosing oversized lenses is often a good idea. This style of beam expander is called Galilean. Two positive lenses can also be used in a Keplerian beam expander design, but this configuration is longer than the Galilean design.
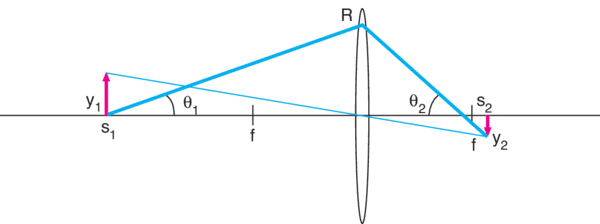
This application is one that will be approached as an imaging problem as opposed to the focusing and collimation problems of the previous applications. An example might be a situation where a fluorescing sample must be imaged with a CCD camera. The geometry of the application is shown in Figure 4. An extended source with a radius of y1 is located at a distance s1 from a lens of focal length f. The figure shows a ray incident upon the lens at a radius of R. We can take this radius R to be the maximal allowed ray, or clear aperture, of the lens.
 Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details
Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details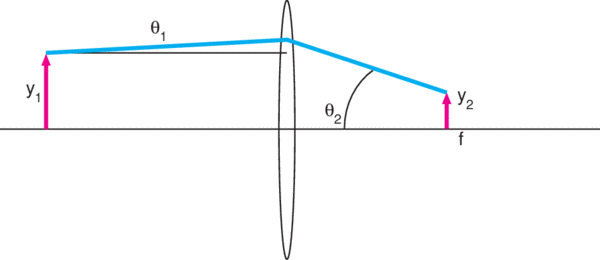
 Ultra-High Velocity
Ultra-High Velocity