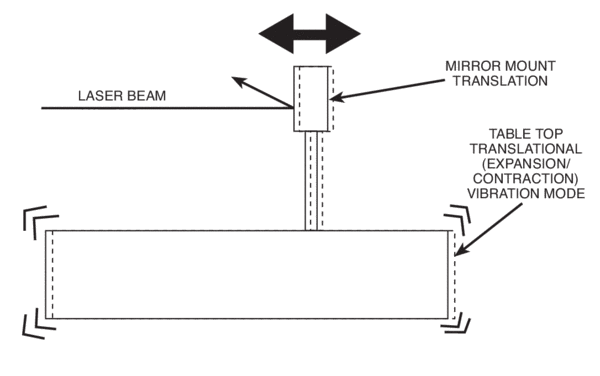
A more serious situation arises when the slope of the table top is considered in the calculation. When a table top or breadboard is affected by vibration, it not only exhibits translational modes, it also has bending modes. Table top bending can have serious consequences for optical performance for two reasons:
- When a mirror is rotated, the angle of the reflected beam is twice the tilt angle.
- The “doubled” error also increases linearly with reflected spot distance from the mirror, or:
δtilt = θmirror x ×
Where:
δtilt = spot displacement
θmirror = mirror tilt angle
× = distance from the mirror to spot
For example, a tilt of only one milliradian (1 x 10-3 radian) of a flat mirror at a distance of one meter produces a shift in the reflected beam of 2 mm!
Note: We greatly appreciate the participation of Dr. Daniel Vukobratovich of the Optical Sciences Center at the University of Arizona who supplied this mathematical treatment.
The maximum slope of the table is also quite easy to determine. As an example, consider a 4 ft x 8 ft x 12&in. (1200 x 2400 x 305 mm) Newport RS 2000™ table. The table is supported at each corner and is excited by a PSD of 10-9g2/Hz. In this idealized case the table acts like a simply supported, uniformly loaded beam, and maximum surface slope is related to maximum table deflection by:
 Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details
Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details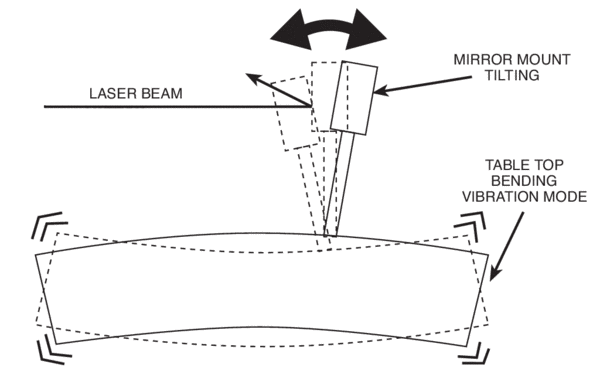
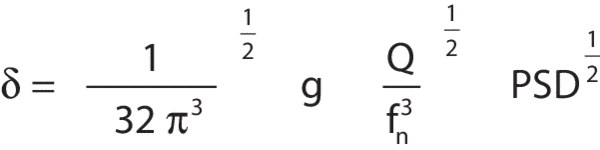
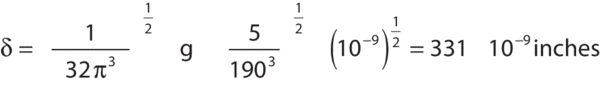
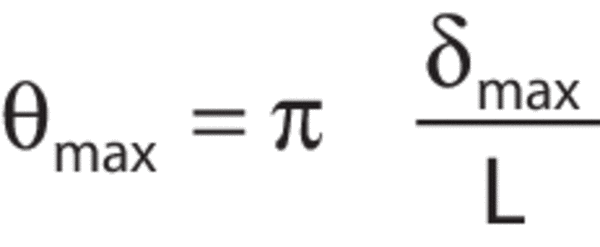
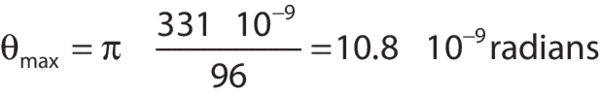
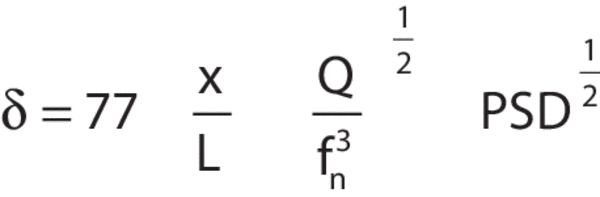
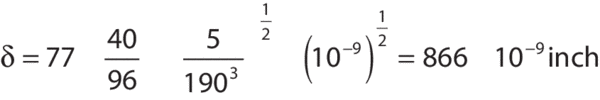
 Ultra-High Velocity
Ultra-High Velocity