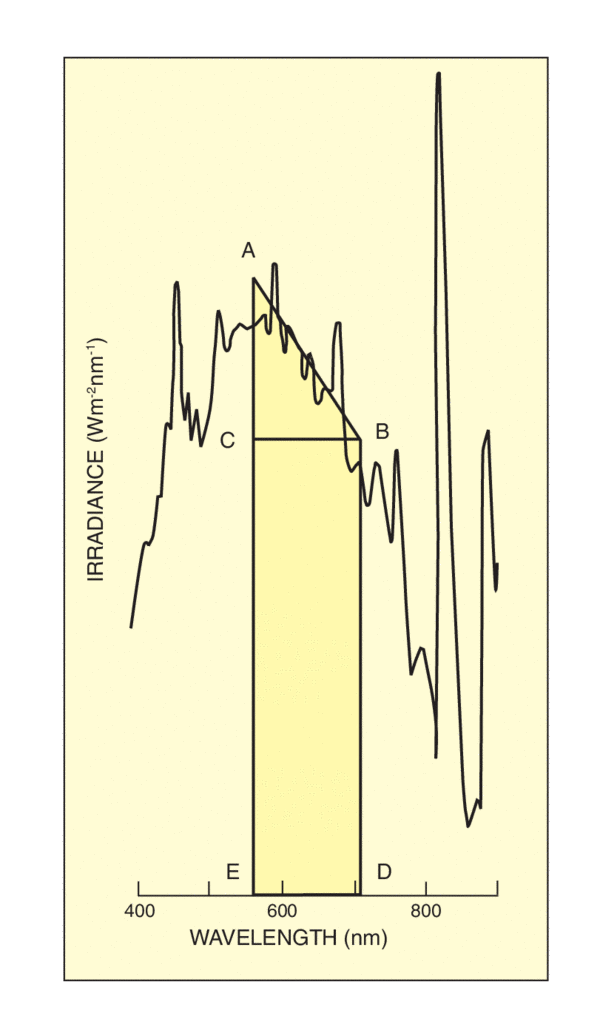
Step 1: Determine the irradiance in the specified spectral region by measuring the area under the curve over the specified wavelength range. We use the curve shown. Note that this curve is for a simulator with a 4 x 4 inch (102 x 102 mm) beam. Our example is for a 2 x 2 inch (51 x 51 mm) beam.
We drew the line AB as best estimate of the average of the curve from 680 - 720 nm. Use a photocopier with magnification to make this area measurement easier. The area under the curve is approximately the sum of the area of the triangle ABC and the rectangle CBDE. We use simple scaling of the axes to find CE, and AC.
Area ABC = 140 x 0.5 x 0.82 = 57.4 W m-2
Area CBDE = 140 x 3.16 = 442 W m-2
Total area, ABC + CBDE, = 499 W m-2
The total irradiance or power density is 499 W m-2 for a 4 x 4 inch simulator. Since our example deals with a 2 x 2 inch model, we must multiply the output by the relative outputs of these two models, i.e. 10360/2765 = 3.75
499 W m-2 x 3.75 = 1871 W m-2
Step 2: Find out how much power falls on the sample.
The irradiated area is 0.02 m x 0.02 m = 0.0004 m2, so the total radiation falling on the sample is
0.0004 m2 x 1871 W m-2 = 0.75 W
Step 3: Calculate the dose, i.e. the total energy that falls on the sample in 1.5 minutes. The dose is the power multiplied by the exposure time, 90 seconds
0.75 W x 90 s = 67.5 J (1 Ws = 1 J)
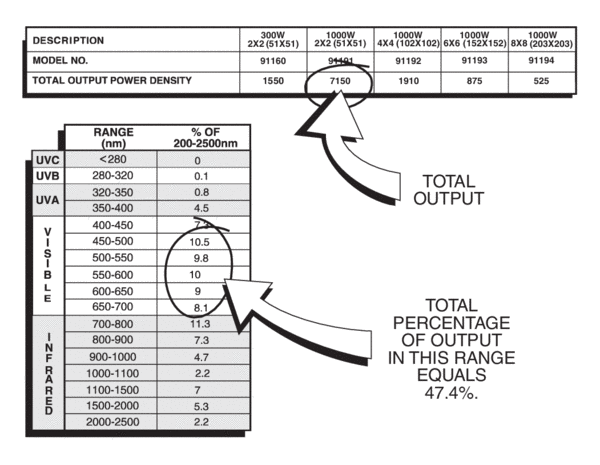
Find the irradiance in the wavelength range 450 - 700 nm from a 91191, 2 x 2 inch kW simulator with AM 1.5 Global Filter.
Step 1: Find what fraction of the output is in the specified range. (Figure 2 shows the tabled data.) The total percentage of the output in this range = 47.4%
Step 2: Multiply the fraction by the total power.
The top table in Figure 2 shows the total output power density to be 7150 W m-2 for this model. Therefore the irradiance for the 450 - 700 nm range is:
0.474 x 7150 = 3389 W m-2
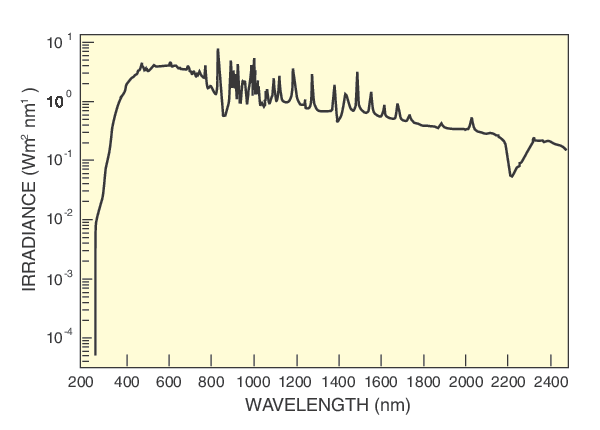
Most of our plots are linear plots. Log-lin plots are useful to illustrate the fall-off of the irradiance at the atmospheric edge because the log scale enhances the low value data and compresses the high value data. Plotting Figure 1 as a log-lin plot makes the entire spectrum look flatter as the peaks are reduced. When two plots, such as solar and simulator irradiance are both plotted on the same log-lin grid, differences appear less.
 Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details
Over 8,000 products in-stock! & FREE 2-Day shipping on all web orders!* Learn More FREE T-Shirt with orders $250+ Details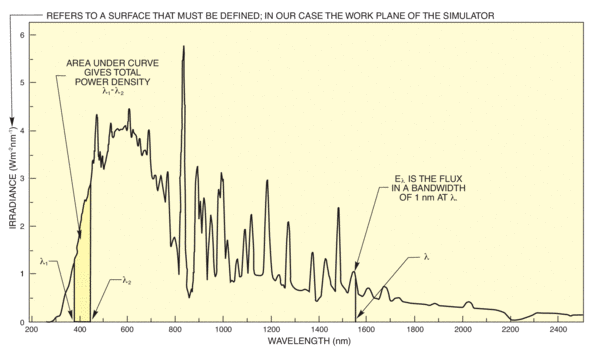
 Ultra-High Velocity
Ultra-High Velocity